Ik heb ergens een vage bevatting van het concept: iets dat er op één manier ingewikkeld uitziet, kan omgezet worden naar iets dat er op een andere manier eenvoudig uitziet, en omgekeerd.

Met geluid kan ik het mij zelfs aanschouwbaar voorstellen: iets dat er als een heel raar ding uitziet, kan gezien worden als een optelling van allemaal simpele tonen die een propere sinusgolf doen:

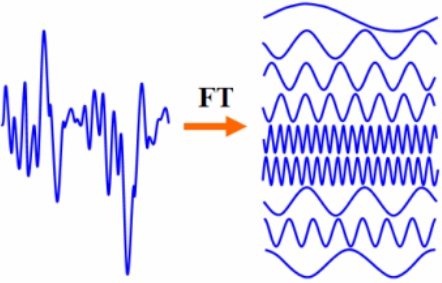
't Is natuurlijk ongetwijfeld allemaal moeilijker dan ik het mij voorstel, maar als zo'n ingewikkeld ding omgezet is naar een reeks meer eenvoudige dingen, dan kan het omgekeerde ook. En dus is het bijvoorbeeld mogelijk om in de getransformeerde gegevens patronen te zien, die er uit te wippen, en dan weer terug te keren naar een opgekuist origineel. 

Enter de Fast Fourier Transform / Inverse Fast Fourier Transform voor in Photoshop!

Men neme een foto zoals deze van mijn nonkel Felix en zijn nichtje Marilka ergens in de jaren 1930, twintig of zo jaar geleden ingescand van een blinkend origineel met een afgrijselijk patroon op het fotopapier:

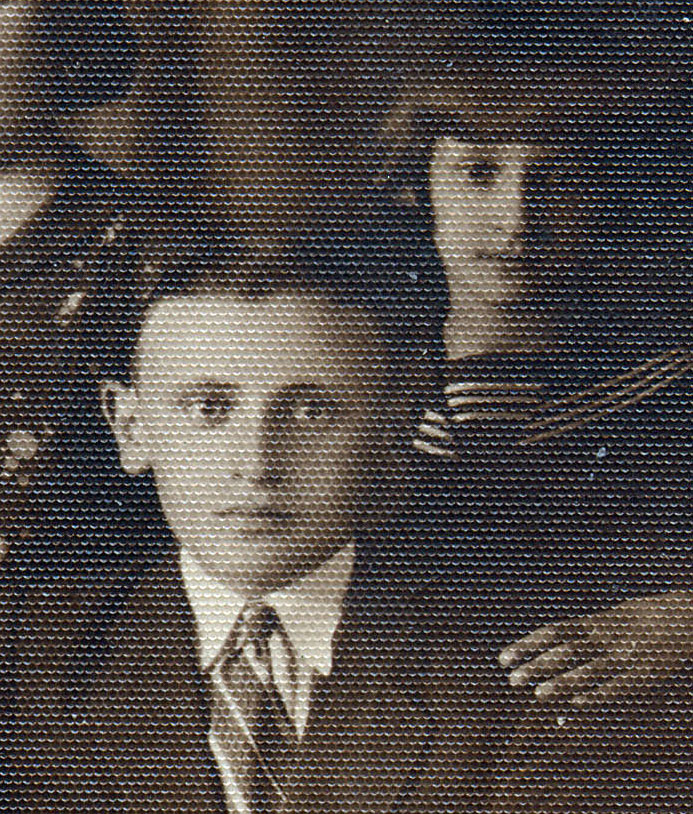
Onbegonnen werk om die schubben met de hand weg te krijgen. Onbegonnen werk om met een combinatie van blur en iets anders te proberen te futzen. 

Maar geen onbegonnen werk als de hele foto ge-fast-fourier-getransformeerd wordt. Elk periodiek patroon dat over heel het beeld zit, komt in de transformatie uit als een paar pieken, die te verwijderen kunnen zijn.

Dat ziet er dan zo uit:

…wat niet veel zegt, ahem ja. Maar als we naar het rood-kanaal gaan kijken, ziet, daar staan die pieken dus in:

Als ik een andere foto neem waar zo geen herhalend patroon op staat en ik transformeer die, dan zie ik iets helemaal anders:

En wat graadt gij? Jawel: het roodkanaal van een foto-met-viezigheid er uit laten zien als een foto-zonder-viezeigheid, dat doet aangename dingen als er dan een omgekeerde transformatie op gedaan wordt.

Men neme een patroon zoals dat met al die kruisjes erop, men manipulere dat een beetje dat waar nu lichtere patronen staan (op het centrum na!), er zwart komt te staan:

Dan plakke men al wat zwart is over het roodkanaal, en een inverse fast fourier transform later ziet die foto van helemaal bovenaan er zo uit:

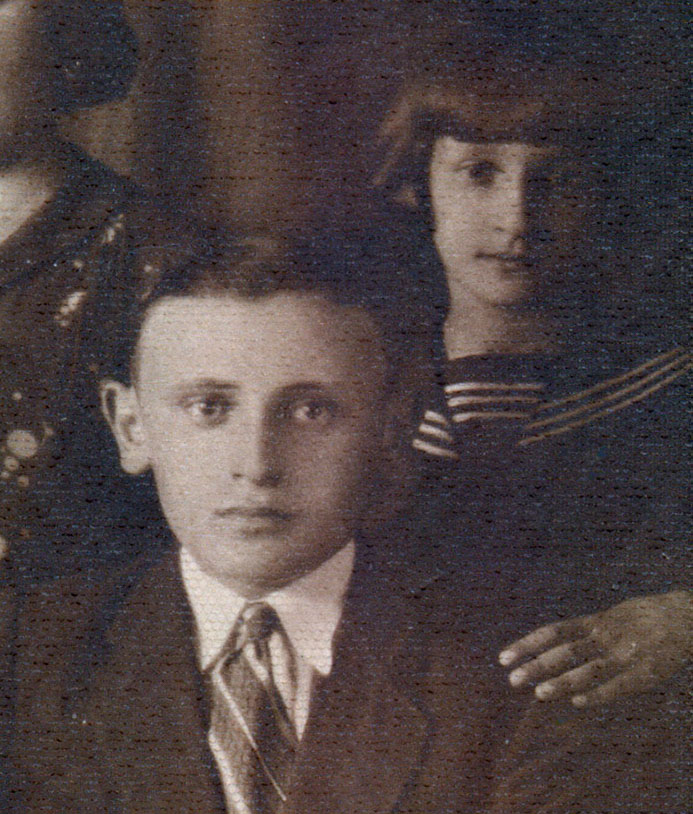
Nee, nog altijd niet perfect. Maar toch: een enorm verschil. Met nog wat prutsen en zoeken, komt dat ongetwijfeld nog in orde.